在19世纪数学分析从“直观”走向“严谨”的关键转型中，魏尔斯特拉斯提出的“一致收敛”概念，是解决此前理论矛盾、筑牢分析基础的核心突破，其对数学分析研究的意义，集中体现在三个维度。

首先，它解决了“逐项运算”的逻辑漏洞，统一了收敛性判定标准。在一致收敛概念出现前，数学家们常直观地认为“收敛函数项级数可逐项求导、逐项积分”，但实际存在大量反例——如傅里叶级数中，收敛的级数逐项积分或求导后可能发散，导致分析运算陷入“时而成立、时而失效”的混乱。魏尔斯特拉斯通过“一致收敛”的严格定义（即对任意给定的误差，存在一个与自变量无关的“公共N”，使得所有项都能同时满足误差要求），明确了逐项求导、逐项积分、极限交换等运算成立的充要条件，让这些核心操作有了统一且严谨的判定依据，终结了此前依赖直观的“随意性”。

其次，它推动了函数概念的深化，拓展了分析研究的对象。在19世纪前，数学分析的研究对象多局限于连续、可导的“ nice 函数”（如多项式、三角函数）。而魏尔斯特拉斯借助一致收敛，构造出首个“处处连续但处处不可导”的函数——该函数由一致收敛的级数定义，却打破了“连续函数必可导”的直观认知。这一突破不仅颠覆了传统函数观，更让分析学的研究范围从“光滑函数”扩展到更广泛的“抽象函数”，为后续实变函数、泛函分析等分支的诞生埋下伏笔。

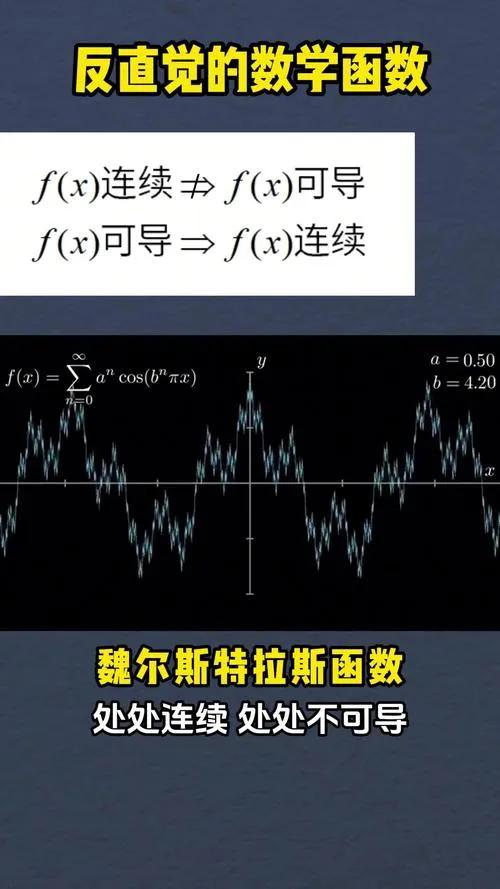
最后，它奠定了数学分析的严谨化范式，影响了整个现代数学的逻辑体系。魏尔斯特拉斯以“ε-N”“ε-δ”语言为核心，将“一致收敛”嵌入分析基础，使极限、连续、积分等核心概念摆脱了对“运动”“无穷小”的直观依赖，转为纯粹的逻辑符号表述。这种“严格化”范式不仅让数学分析告别了“悖论丛生”的阶段，更成为现代数学的标准范式——从复分析到拓扑学，诸多分支都以“一致收敛”式的严谨逻辑为基础，推动数学从“经验科学”走向“演绎科学”。

综上，“一致收敛”不仅是解决具体分析问题的工具，更是重塑数学分析逻辑基础、拓展研究边界的“里程碑”，其影响贯穿至今，仍是学习和研究现代分析的核心概念之一。

#科学技术史#​