在极坐标和直角坐标的互化中x=ρcosθ，y=ρsinθ所以x+y=1化成的极坐标方程为ρcosθ+ρsinθ=1极坐标方程实际上，极坐标与直角坐标一样，都是为了表示点在空间中的位置而引入的参照系直角坐标和极坐标互化公式x = ρcosθ，y = ρsinθ，ρ#178=x#178+y#178 一般。

二重积分经常把直角坐标转化为极坐标形式，主要公式有x=ρcosθ y=ρsinθ x^2+y^2=ρ^2 dxdy=ρdρdθ，极点是原来直角坐标的原点以下是求ρ和θ 范围的方法一般转换极坐标是因为有x^2+y^2存在，转换后计算方便，题目中会给一个x，y的限定范围，一般是个圆，将x=ρcosθ y=ρsinθ。

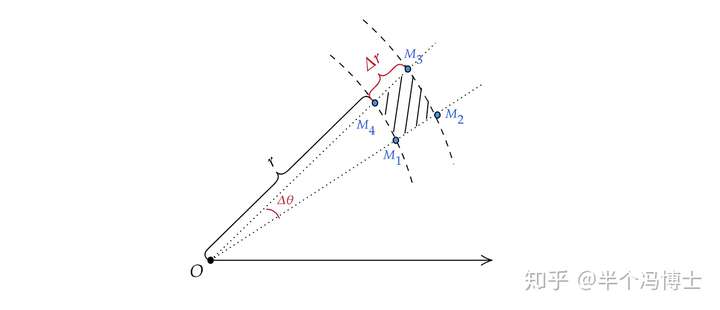
在直角坐标与极坐标的互化中，dxdy = rdrdθ 的原因主要在于两者描述的微小面积相等，且它们实际上表示的是向量分析中的楔积或外积具体解释如下直角坐标系中的微小面积在直角坐标系中，dx 和 dy 分别表示沿着 x 轴和 y 轴的微小增量一个微小矩形区域的面积可以用 dx 和 dy 的乘积来表示。