公式cosx = e^ + e^ 2解释该公式表示余弦函数cosx可以通过复数指数函数e^和e^的和除以2来得到同样地，e是自然对数的底数，i是虚数单位欧拉公式是将三角函数与复数指数函数相关联的重要公式，在复分析领域有着广泛的应用这一公式由莱昂哈德·欧拉提出，并以他的名字命名欧拉公式不仅在数学领域有着重要地位，还在力学光学和天文学等多个领域有着广泛的应用。

ex与三角函数的关系是欧拉定理高等代数中使用欧拉公式将三角函数转换为指数sinx=e^ixe^ix2i cosx=e^ix+e^ix2 tanx=e^ixe^ixie^ix+ie^ix在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许它们的取值扩展到任意实数。

高等代数中使用欧拉公式将三角函数转换为指数由泰勒级数易得sinx=e^ixe^ix2i cosx=e^ix+e^ix2 tanx=e^ixe^ixie^ix+ie^ixcosα=12e^iα+e^iαsinα=i2e^iαe^iα泰勒展开有无穷级数，e^z=exp。

欧拉公式揭示了一个深刻的关系，即在复数领域中，余弦函数cos x可以用指数函数的形式来表达，具体公式为cos x = e^ix + e^ix 2其中，e是自然对数的底，i是虚数单位这个公式不仅扩展了三角函数的定义范围，而且还展示了三角函数和指数函数之间内在的联系在复变函数论的探讨中，欧拉公式。

#160#160e^ix=cosxisinx，然后采用两式相加减的方法得到sinx=e^ixe^ix2i，cosx=e^ix+e^ix2欧拉公式又称为欧拉定理，也称为尤拉公式，是用在复分析领域的公式，欧拉公式将三角函数与复数指数函数相关联，之所以叫作欧拉公式，那是因为欧拉公式是由。

sinx和cosx的欧拉公式写法如下cosx的欧拉公式公式$cos x = frace^ix + e^ix2$解释该公式通过欧拉公式$e^ix = cos x + i sin x$及其共轭$e^ix = cos x i sin x$相加并除以2得到，它展示了余弦函数与复数指数函数之间的关系sinx的欧拉公式公式$sin x。

高等代数中三角函数的指数表示由泰勒级数易得sinx=e^ixe^ix2i cosx=e^ix+e^ix2 tanx=e^ixe^ixie^ix+ie^ix泰勒展开有无穷级数，e^z=expz＝1＋z1＋z^22＋z^33＋z^44＋＋z^nn＋ 此时三角函数。

它将三角函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位将公式里的x换成－x，得到e^ix=cosxisinx，然后采用两式相加减的方法得到sinx=2i，cosx=2注意欧拉公式不仅仅是看起来优美，用起来也是无比重要学信号分析的，欧拉公式是必备工具。

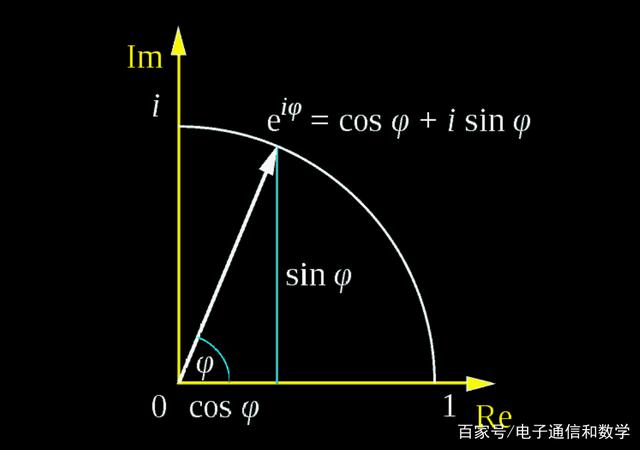
欧拉定理e^ix=cosx+isinx其中e是自然对数的底，i是虚数单位它将三角函数的定义域扩大到复数，建立了三角函数和指数函数的关系，它在复变函数论里占有非常重要的地位将公式里的x换成x，得到e^ix=cosxisinx，然后采用两式相加减的方法得到sinx=e^ixe^ix2i。

这是欧拉公式复变函数中，e^ix=cos x+isin x称为欧拉公式，e是自然对数的底，i是虚数单位拓扑学中，在任何一个规则球面地图上，用 R记区域个 数 ，V记顶点个数 ，E记边界个数 ，则 R+ V E= 2，这就是欧拉定理 ，它于 1640年由 Descartes首先给出证明 ，后来 Euler欧拉。

欧拉公式在不同的数学领域中展现出了多样的形式在复变函数论中，欧拉公式被表述为eix=cosx+isinx，其中e是自然对数的底，i是虚数单位这个公式将三角函数的定义域扩大到了复数，建立了三角函数和指数函数之间的联系将x换成x，可以得到eix=cosxisinx通过这两个公式，我们可以推导出sinx和cosx。

接下来是复数形式的欧拉公式，由eix = cosx + isinx得出，从中我们能够得到sinx和cosx的具体表达式，即sinx = eix eix 2i，cosx = eix + eix 2这是复数理论中的一个重要公式，它将三角函数与指数函数联系起来在几何学中，欧拉公式也发挥着重要作用例如，对于任意三角形。

cosx=1x^22！+x^44！x^66！++1^k*x^2k2k！+ lt3 将lt1式中的x换为ix，得到lt4式将i*lt2+lt3式得到lt5式比较lt4lt5两式，知lt4与lt5恒等于是我们导出了e^ix=cosx+isinx，将公式里的x换成x，得到e^ix=cosxisinx，然后采用两。