1、e的y次方减e等于0e是数学常数,是自然对数函数的底数有时称它为欧拉数,以瑞士数学家欧拉命名数学,是研究数量结构变化空间以及信息等概念的一门学科数学是人类对事物的抽象结构与模式进行严格描述推导的一种通用手段,可以应用于现实世界的任何问题,所有的数学对象本质上都是人为定义的。
2、当 y 等于 0 时,e 的 0 次方减去 e 就等于 1 减去 e,结果为 e 1这通常不等于 0,除非 e 的定义取 1,但常规定义中 e 大于 1如果 y 是正数,比如 y = 1, 2, 3 等,e 的 y 次方将是一个大于 1 的数,减去 e 后会得到一个正差值,表示增长的幅度例如,e 的 2。
3、因此,e的X次方可以写成y=1e^x这样做的原因是,指数函数和对数函数是互为反函数的,它们的定义和性质是相互联系的自然对数的底数e是指数函数e^x的底数,而自然对数lnx是指数函数的反函数,即lne^x=x因此,我们可以利用指数函数的倒数来消去e,得到我们想要的形式总之,如果。
4、x和y换一下不就得到2x=e的y次方减e的负y次方设e的y次方等于t所以t+1t=2x,就是t22tx+1=0解得t=x加减根号下x21因为原函数的值域就是反函数的定义域2分之e的x次方减e的负x次方根据基本不等式是大于等于1。
5、具体来说,\e^y\ 和 \e^y\ 分别表示的是 \e\ 的 \y\ 次方和 \y\ 次方,这两个表达式之间没有任何乘法关系,因此不能使用指数相加的规则换句话说,\e^y + e^y\ 不能简化为 \e^y + y = e^0 = 1\实际上,这个表达式是一个常见的。
6、图像如下图所示,互为倒数的两个函数图像没有必定的关系函数,最早由中国清朝数学家李善兰翻译,出于其著作代数学之所以这么翻译,他给出的原因是“凡此变数中函彼变数者,则此为彼之函数”,也即函数指一个量随着另一个量的变化而变化,或者说一个量中包含另一个量背景 十七世纪伽俐略在。
7、将原函数$y = frace^x e^x2$进行变形,得到$y = frace^2x 12e^x$令$e^x = t$,则原方程转化为关于$t$的一元二次方程$t^2 2yt 1 = 0$解此方程得到$t = y pm sqrt1 + y^2$由于$e^x$的值域为正实数,因此选择正根。
8、等式两边取以e为底的质数因为e^lnx=x然后由你写的“由”后面第一个等式,左边为e^y,右边为x+根号下的1+x^2故有你写的那个结果。
9、要把e的x次方中的e去掉,可以通过使用自然对数的定义来实现具体来说,自然对数lnx定义为e的多少次方等于x,即e^y=x,则lnx=y因此,我们可以将e的x次方写成e^lnx*x,这样就把e去掉了实际解答方式和对策在进行数学计算时,如果需要去掉e,可以通过上述方法来实现,将e的次方转化为自然。
10、自然对数ln是以e为底的对数函数,即如果y=lnx,那么e的y次方等于x,可以写作x=e^y其次,e的数学意义在于它是一系列等比数列的极限,这些数列的比值恰好等于1e换句话说,e是单位时间内持续翻倍增长。
11、e^x e^x =32 把e^x当做一个整体Y,也就是 Y 1Y =32 Y=2 或 12 舍去所以e^x=2 x=ln2。
12、20170707 从e的2x次方减二倍y乘以e的x次方减1=0解出,怎么解到下 11 20200430 微分方程y的二阶导数减去2×y的一阶导数减去e的2x次幂等于 20200430 求微分方程y的二阶导数减去2×y的一阶导数减去e的2x次幂等 20120621 微分方程e的2xy次方dx减去e的x+y次方dy=0的通解。
13、e的x次方1的导数即e^x1的导数就等于e^x导数Derivative,也叫导函数值又名微商,是微积分中的重要基础概念当函数y=fx的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f’x0或。
14、简单计算一下即可,答案如图所示。
15、由于$e^x$是指数函数,其值域为$$,即$e^x$恒大于0分析$frac1e^x$的性质由于$e^x$恒大于0,所以$frac1e^x$也恒大于0分析$Y = 1 frac1e^x$的值域由于$frac1e^x$恒大于0,所以$frac1e^x$恒小于0因此,$1。
16、e的3次方等于e的立方,约为2008554 e的1次方。
17、这个不一样啊 最简单的验证方法就是代数法 令y=1,带入上式,就有 e^1和1e^1e^1=e 1e^1=1e=e^1所以,他俩不一样的啊。
转载请注明来自德立,本文标题:《e的y次方减e等于多少》

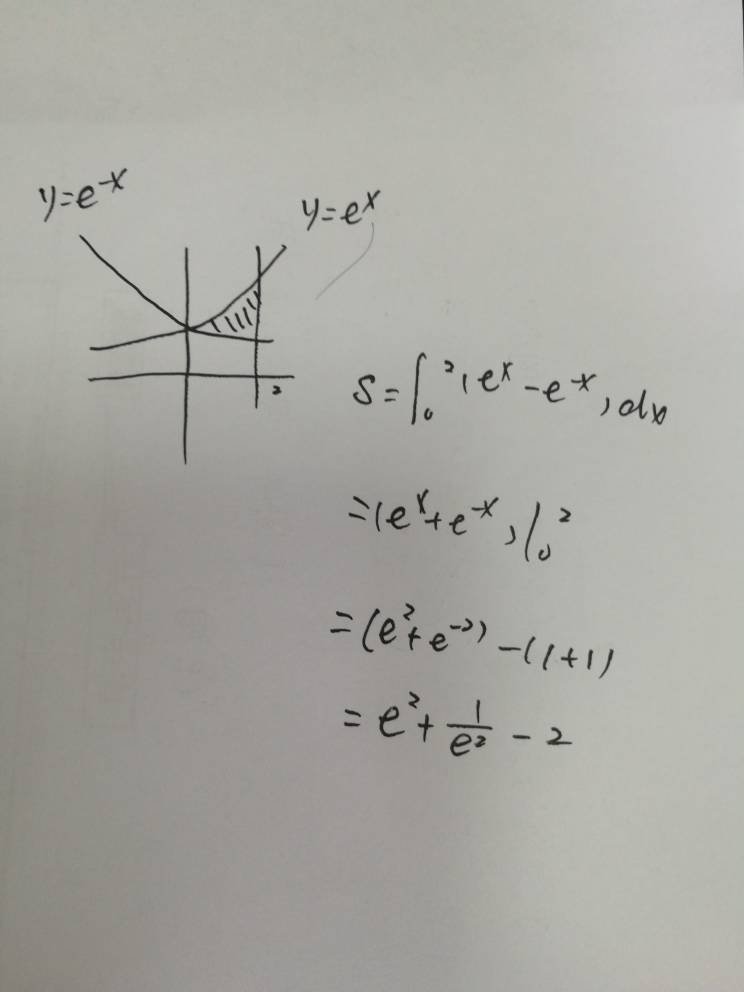

 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号
还没有评论,来说两句吧...